From Moves to Models
The importance of rich learning environment
In a previous blog post, I discussed a study demonstrating how the quality of chess players’ decisions is influenced by the improvement in the tools and materials available for learning the skill. A supportive and stimulating environment plays a crucial role in fostering good work and high-quality decisions. This year, I experienced this firsthand. My environment was enriched by the opportunity to supervise the MSc dissertations of two outstanding students, Elisa Solaris and Justin Ong.
Elisa focused on developing and applying Natural Language Processing models, specifically utilizing BERTopic to analyze Reddit data (a preprint will be available soon). Meanwhile, Justin pushed the boundaries of our knowledge, understanding, and analytical skills by creating a model to estimate the complexity of chess positions during the middlegame stage.
Why the chess middlegame?
Simply put, it is one of the most complex and unpredictable phases of the game. The tree of possibilities expands exponentially, reaching a level where any comprehensive analysis becomes virtually impossible. You’ve likely heard it before: “There are more possible chess games than atoms in the Universe” Shannon number.
The strategic structure of chess is traditionally divided into three phases: the opening, middlegame, and endgame. The opening phase is characterized by reduced variability due to established theoretical lines, while the endgame involves sparse positions that are often amenable to exhaustive analysis. In contrast, the middlegame stands out as uniquely challenging. This complexity and unpredictability are precisely what make the middlegame such a fascinating focus for research in chess strategy and decision-making.
To address the complexity and sparsity of signals in the middlegame, Justin approached the problem from a cognitive psychology perspective. He explored literature behing planning depth of chess players, discovering that they typically plan two to six steps ahead. He also took into account that players tend to chunk semantically related chess pieces and constellations, effectively organizing their vast domain-specific knowledge.
Building on this insight, Justin focused on defining the size of chess constellations or patterns. By borrowing the Sliding Window algorithm from Natural Language Processing, he analyzed a dataset of 2,235,823 games. This process yielded 106,810 unique 11-ply constellations that appeared at least 20 times in the data. This innovative approach allowed him to capture and analyze recurring patterns within the complex middlegame phase.
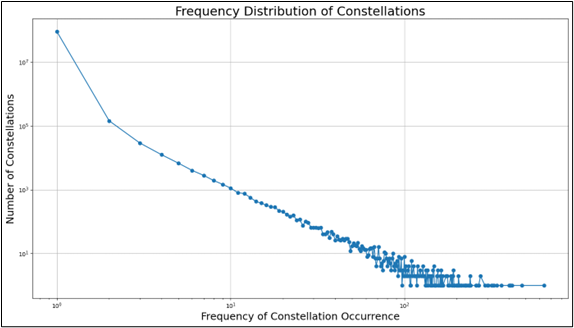
Complexity in chess
In addition to innovative methodological pipeline, Justin conducted a comprehensive review of studies that have attempted to quantify position complexity in chess. He identified three commonly used proxies for complexity:
Difficulty: The challenge faced when playing from an advantaged or disadvantaged position.
Optionality: The cognitive effort required to find an optimal move during the decision-making process.
Rarity: The frequency of occurrence of a given chess position.
Building on this literature review, we defined these metrics as follows:
Difficulty was quantified using the board centipawn score calculated by chess engines.
Optionality was measured by the number of nodes searched by the chess engine to identify the best move.
Rarity was determined using Inverse Document Frequency (IDF) scores of chess constellation appearances across all games in the dataset.
Classifier
Finally, Justin used these measures to train a multinomial regression model to predict the quality of chess decisions. Decision quality was categorized according to the Lichess classification of blunders, mistakes, inaccuracies, and optimal moves. This approach provided a nuanced framework for understanding how various facets of positional complexity influence the decision-making process in chess.
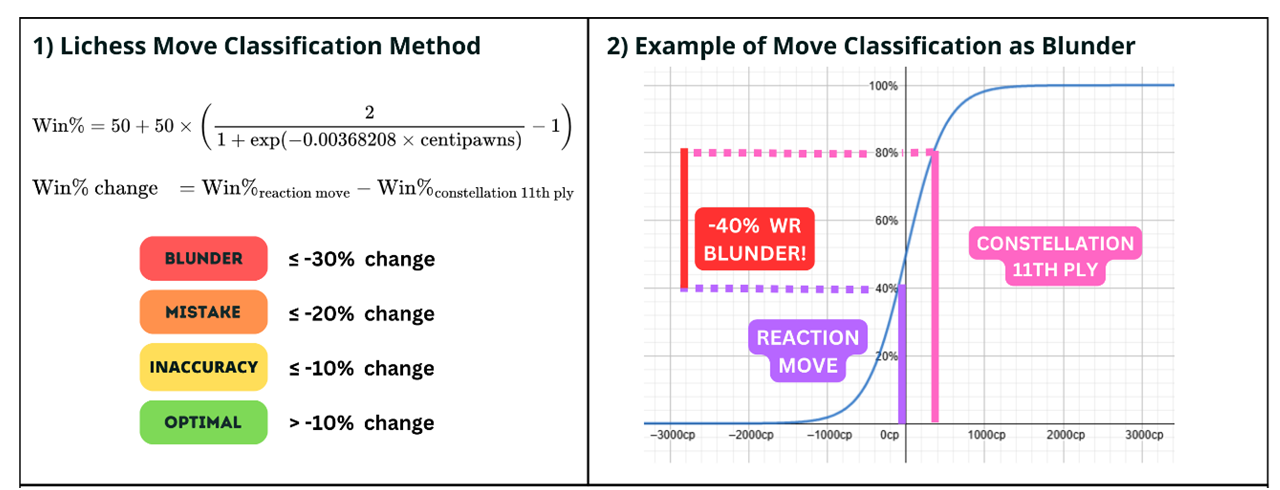
Quality of decisions
The MLR model, based on the proposed constellation complexity scoring system, demonstrated good predictive power for players’ decision quality. The model achieved an overall weighted F1 score of 0.75, with a weighted precision of 0.84 and a weighted recall of 0.70. The model’s performance varied across move types, as illustrated by the ROC curves. These curves demonstrate the model’s discriminative ability, showing a high AUC for Blunder (0.97), Optimal Move (0.86), and Mistake (0.87), but lower for Inaccuracy (0.60).
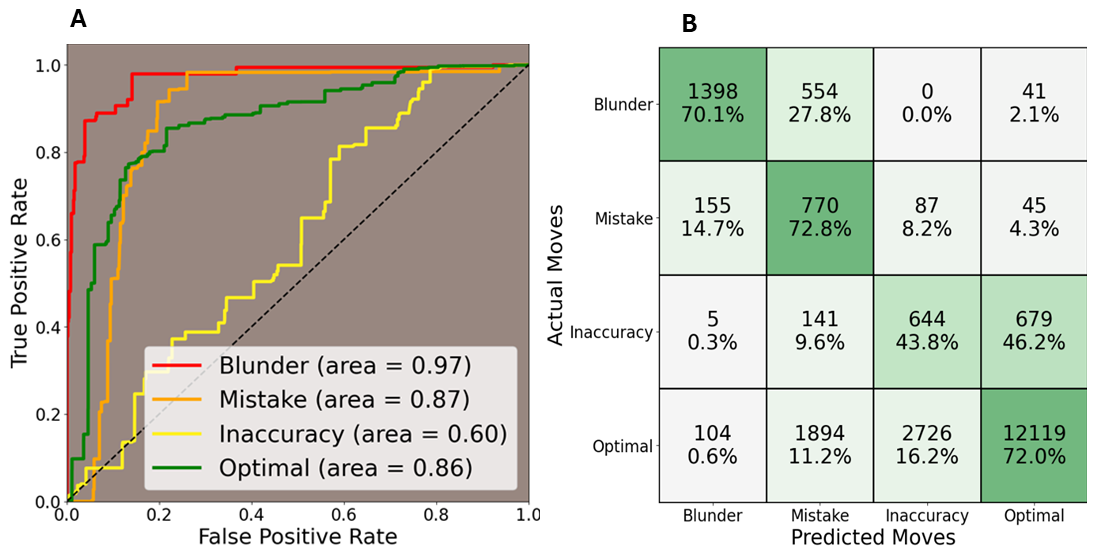
What did we learn?
Through his work, Justin went beyond simply building a model; he also provided valuable insights into the types of moves and the significance of each predictor in relation to different types of errors. By examining the strength of each predictor, he shed light on what these findings could mean for chess players aiming to improve their decision-making and understanding of positional complexity.
Here is the link for the preprinted paper, ENJOY: LINK